橡膠的疲勞壽命，是指橡膠制品在受到周期性的拉伸、壓縮或剪切變形時，抵抗內部或表面產生裂紋并導致其最終斷裂的能力，通常用達到破壞時所經歷的變形循環次數來表示。

疲勞壽命研究主要分為裂紋形核法和裂紋擴展法兩大分支。裂紋形核法關注從微觀缺陷到宏觀裂紋形成的過程，而裂紋擴展法則聚焦已有裂紋的增長規律。兩種方法在理論基礎、實驗技術和應用場景上各有側重，共同構成了橡膠疲勞壽命預測的完整體系。

本文將詳細分別介紹裂紋形核法與裂紋擴展法，包括以下內容：

1.裂紋形核法

1.1 基本介紹

1.2 應變比對壽命預測的影響

1.3 累計疲勞損傷準則

1.4 隨機載荷下的疲勞壽命

2.裂紋擴展法

3.總結

1.裂紋形核法

1.1 基本介紹

裂紋形核法基于微觀損傷累積理論，認為疲勞失效是循環載荷下微觀缺陷逐步演化的結果。

裂紋形核法的核心機制：分子鏈斷裂，填料脫粘，應力集中效應。

裂紋形核法試件通常長這樣，特征是試件上無初始缺陷：

對于橡膠來說，通常考慮獲取其e-N曲線，也就是應變幅值-壽命曲線，通過向試件施加不同幅值的正弦載荷，獲取整條e-N曲線：

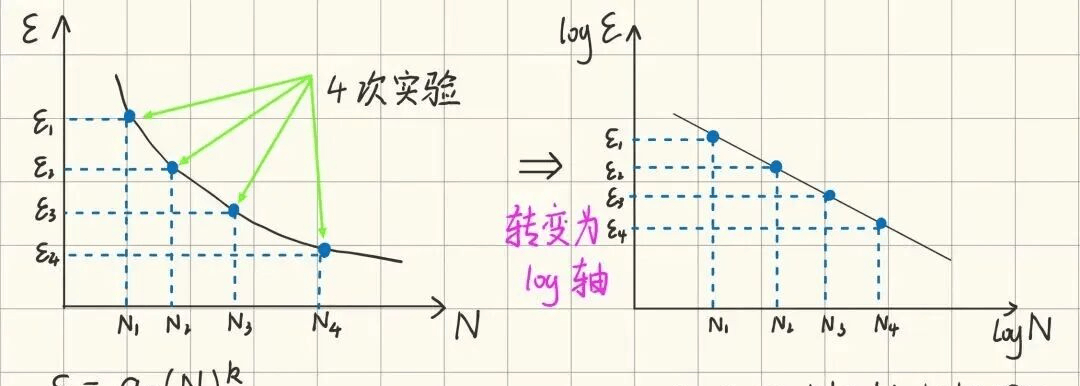
由圖中可觀察得出，載荷幅值ε 與循環次數壽命N之間的關系表示為圖下方的兩種表達式。

特別指出的是，圖中的縱坐標不一定只是載荷幅值，還可以是應變能密度（SED），最大主柯西應力（S_max），開裂能密度（CED），最大主應變（E_max），等效拉伸應變（E_equiv）

此處主要還是詳細討論，e-N曲線求解疲勞壽命的方法。

1.2 應變比對壽命預測的影響

我們知道，在實驗獲取e-N曲線過程中，使用的是不同應變幅值的動載荷，而動載荷最大的特點就是，可以動的參數很多，幅值，頻率，應變比等等。而橡膠e-N曲線縱坐標只有應變幅值，其他信息表示不出來，故而我們有必要規定，e-N曲線中不同的點，對應橡膠動載荷的應變比、頻率不變，應變幅值改變，如下圖所示：

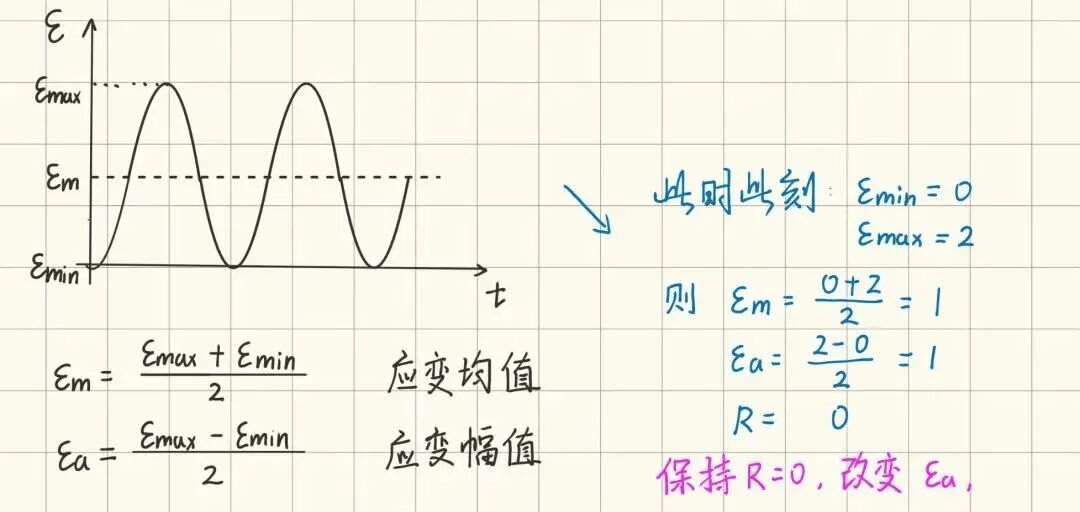
也正因為如此，我們用e-N曲線預測疲勞壽命時候，其實有個隱藏條件，就是應變比是0，比如，應變比是0，應變幅值是2時，壽命是10萬次…

問題來了，假如現在，我們只有應變比R為零時候的e-N曲線，卻想知道應變比R為0.5，應變幅值是3時候橡膠的壽命，怎么辦？

在金屬疲勞壽命領域，有典型的Goodman，Soderberg法則來考慮應變比對疲勞壽命的影響，

橡膠與金屬有所不同，所以要求出等效應變幅值，通常使用Tao提出的方法：

本質上這些公式是求出一個等效應變幅值，代入e-N曲線中，求解壽命。

在Tao方法中，是把應變比R為其他值的動載荷，等效為應變比為R=-1時候的動載荷。但是，對于填充橡膠結構件，建立應變比R=0的等效應變幅值計算模型更為合適。因為，橡膠的e-N曲線，通常是在R=0動載荷下測試獲取的。

故，我們需要對Tao方法，做出改進，如下圖所示：

經過以上操作，求出的等效應變幅值，即為應變比R=0時的等效應變幅值。

1.3 累計疲勞損傷準則

如果，橡膠試件承受的動載荷，是變化的，一會幅值是1，一會兒幅值是3，一會兒應變比為0，一會應變比為0.3，等等，如何求解疲勞壽命？

這就引入了累計疲勞損傷準則，Miner準則，即線性疲勞損傷累積準則。

Miner準則對于載荷的加載順序，載荷的相互作用都不考慮，但是，載荷的加載順序和載荷的相互作用對疲勞壽命的影響，還挺顯著，故而非線性的疲勞損傷累積準則被提出，用來解決這個問題。

此處就不詳細解釋非線性疲勞損傷累積準則的，總之，這些準則的作用，就是用來解決變幅值載荷下的疲勞壽命的。

1.4 隨機載荷下的疲勞壽命

相較于恒幅載荷和變幅載荷工況，隨機載荷工況下橡膠隔振器的疲勞損傷機理更為復雜，且更能反映橡膠隔振器的真實疲勞特性。

載荷塊編制是實現隨機載荷工況下橡膠隔振器疲勞壽命預測的有效手段。載荷塊編 制的基本原理是將全壽命周期下的橡膠隔振器載荷譜編制為多級載荷塊。

載荷塊定義為包含載荷幅值、載荷均值和循環頻次的恒幅載荷分量。因此，基于載荷塊編制的橡膠隔振器疲勞壽命預測的本質是將隨機載荷壽命預測問題轉變為恒幅或變幅載荷疲勞壽命預測問題。

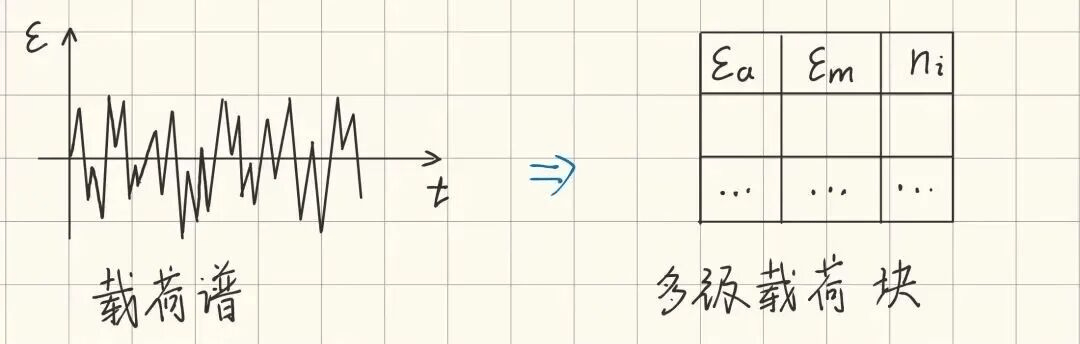
載荷譜統計分析是對載荷譜進行編制的關鍵步驟之一，現有的載荷譜統計方法主要包括穿級計數、峰谷值計數和雨流計數。

雨流計數作為一種雙參數統計方法，可同時統計載荷幅值和載荷均值信息，符合疲勞載荷本身的固有特性。

雨流計數法網上很多專業的講解，此處就不詳細展開了。

隨機載荷下疲勞壽命預測思路大抵如此。

2.裂紋擴展法

裂紋擴展法基于斷裂力學理論，描述已有裂紋在循環載荷下的增長行為。

裂紋擴展法試件通常設置有初始缺陷：

裂紋擴展法，通常是求解裂紋擴展速率，與基于循環最大撕裂能之間的關系，見下圖：

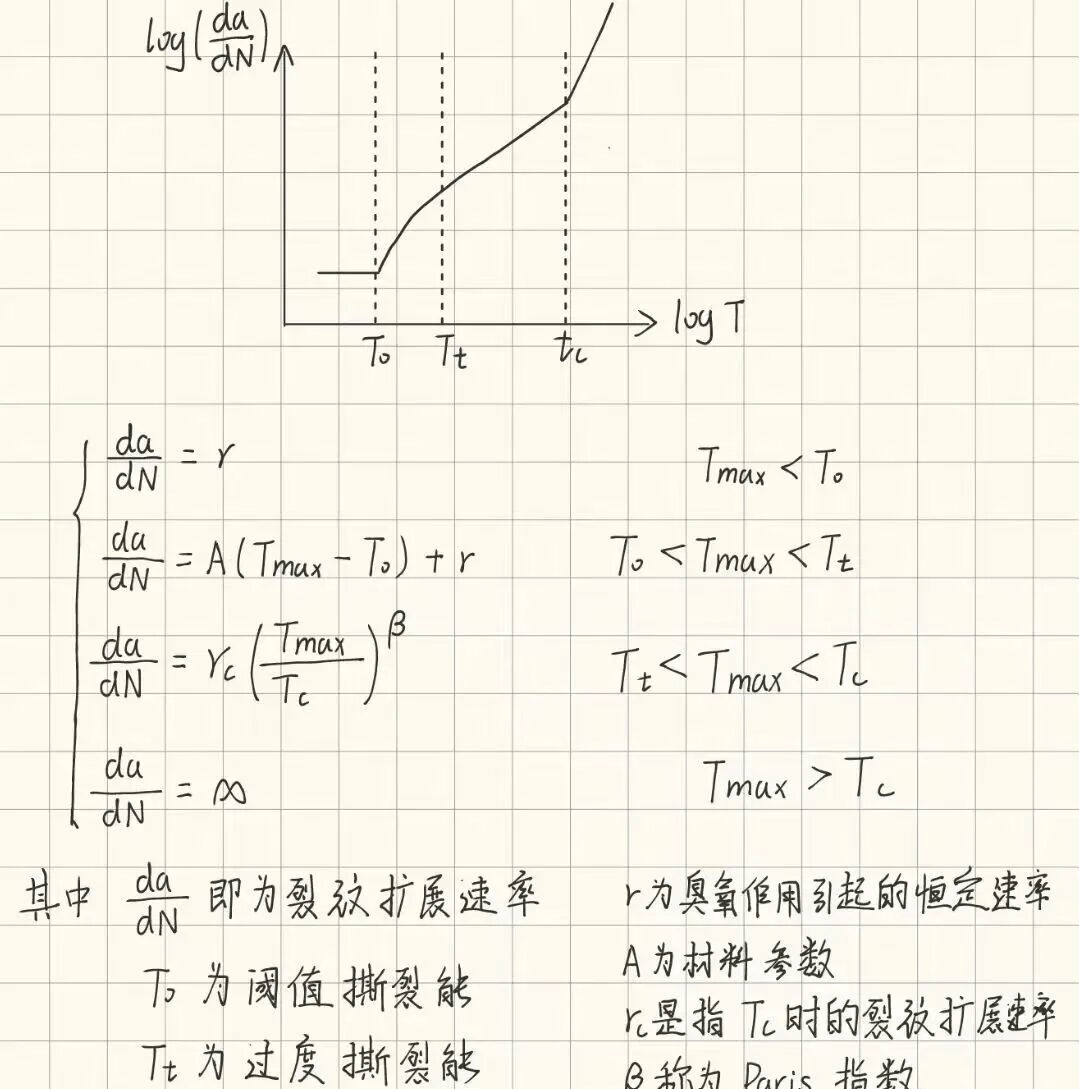
上式實際上表示了裂紋擴展速率與載荷Tmax之間的關系，那現在就存在兩個問題：

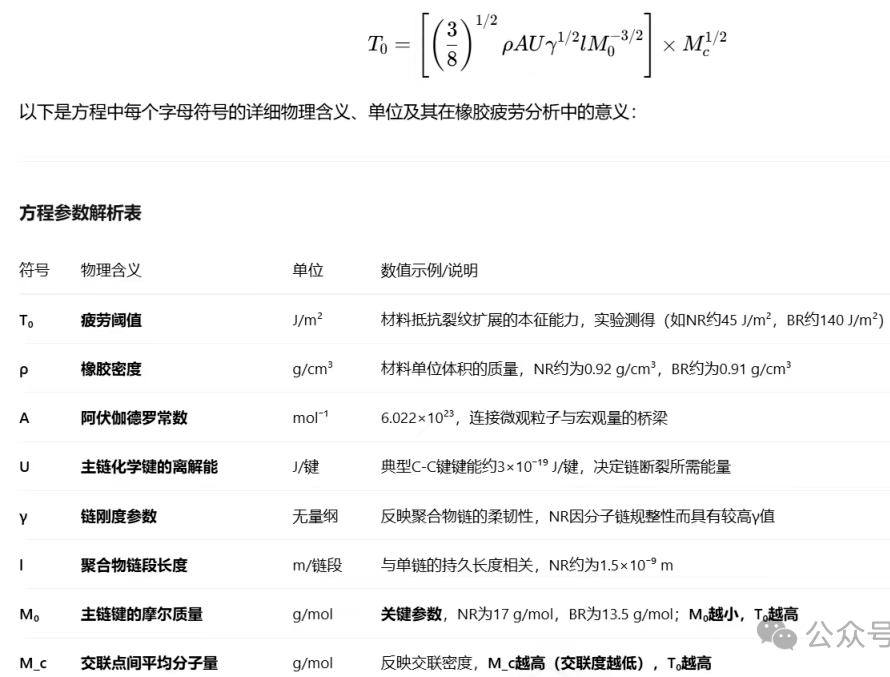
1.式中的未知參數如T0，Tc等，如何獲取？

2.如何根據此式，求解疲勞壽命？

首先解決第一個問題：

裂紋擴展速率與撕裂能之間的關系，即上圖中的曲線，可以通過FCGR測試獲取。

FCGR測試（Fatigue Crack Growth Rate test，疲勞裂紋擴展速率測試）是評估橡膠材料在循環載荷下裂紋擴展行為的關鍵實驗方法。

所謂的FCGR測試，就是對試件施加不同的應變幅值，進而控制不同大小的撕裂能，觀察裂紋的擴展速率，描點，便可獲取整條曲線。

理論上說，獲取整條曲線之后，公式中的未知參數便可直接擬合獲取。

但是獲取整條曲線，需要很多很多次實驗，非常麻煩，故可以使用一些其它招式獲取。

T0為閾值撕裂能，小于該值，壽命無限，可以使用Lake-Yeoh切割法，結合內在強度分析儀（ISA）進行測量。

內在強度分析儀（ISA），其主體結構如圖所示。該儀器能精確控制切割速率和應變，確保測量的一致性。

在室溫下，對復合材料樣品施加幾個應變水平，如2%，4%，8%，10%等，每個應變水平，代表不同的初始撕裂能。

每個應變水平下，以不同的切割速率進行切割，如，10 mm/min、0.1 mm/min、0.01 mm/min。

切割時記錄切割力f，計算切割能F=f/t（t為樣品厚度）；

同步記錄撕裂能T（通過應力-應變曲線積分得到）；

儀器自動記錄每個切割點的T和F，繪制T與F的關系曲線；

記錄曲線與F軸的截距為S0；

代入公式T0=b*S0，求得T0。

Lake-Thomas方程，可以計算T0的理論值，可以與實驗結果對比，觀察是否一致

臨界撕裂能Tc的獲取辦法，簡單很多，對試件施加準靜態拉伸，尋找應力應變曲線中，應力隨應變增加而下降的第一個點。

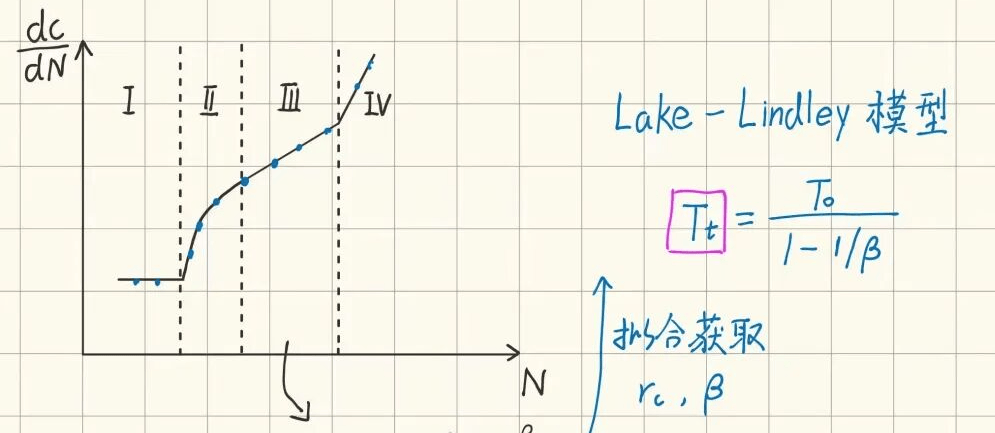
過度撕裂能Tt，為曲線中線性區轉向冪律如的轉折點，通過FCGR測試與Lake-Lindley模型擬合獲得。

總之，使用FCGR測試，可以獲取完整的曲線，使用一些方法，如內在強度分析儀（ISA），可以獲得T0……等等。

針對第二個問題：如何根據這條曲線，求解疲勞壽命？

在疲勞裂紋擴展理論中，整合預先存在的缺陷的擴展速率獲得的，如從其初始尺寸 a0 到臨界尺寸 af所用的循環次數。最準確的疲勞壽命預測是在四種狀態下進行分段積分。捷徑是在缺陷的整個生命周期內假設冪律行為，即III階段。

集成過程詳見下圖：

到此，裂紋擴展法求解疲勞壽命，基本介紹完畢。

3.總結

橡膠疲勞壽命研究的裂紋形核法與裂紋擴展法在理論深度和應用廣度上持續拓展。裂紋形核法通過微觀損傷累積機制揭示疲勞起源，但需解決多軸統計與配方普適性挑戰；裂紋擴展法依托斷裂力學實現高精度預測，模型正從經驗公式向物理信息AI融合演進。實驗技術的革新，特別是多軸高頻測試與原位表征，為模型驗證提供新維度。未來研究需聚焦跨尺度機理貫通、機器-物理模型深度融合以及全壽命預測框架構建，以滿足高性能橡膠構件在工況下的可靠性需求。兩種方法的協同應用將推動橡膠疲勞研究進入智能化、精準化的新階段。